はじめに
以前、当ブログで信用リスク評価法について掲載しました。
信用リスク評価法としては大きく統計モデル、誘導モデル、構造モデルに分類することができることをご説明しましたが、この中でも特に構造モデルはロジックが明快なため説明力が最も高く社会的責任が大きい金融機関での利用に適していることはご説明した通りです。
しかし構造モデルは説明力が高いが精度は低いというデメリットもあります。
そこで今回は構造モデルにフォーカスし、債務超過を許容することでより精度を高めることにチャレンジしてみます。
MertonモデルとBlackCoxモデル
構造モデルはMerton(1974)によりBlack and Scholes(1973)のモデルを応用する形で初めて開発さました(以降、Mertonモデルとします)。
Mertonモデルでは、企業価値が幾何ブラウン運動に従うという仮定の下、株主が企業に対し持つ価値を、企業価値を原資産、負債価値を行使価格としたヨーロピアンオプションとみなしデフォルト確率を算出しています。
しかしここで算出している確率は満期時点に企業価値が負債価値を下回っている、すなわち債務超過する確率であり満期前に債務超過することは考慮されていません。現実には1度債務超過すると銀行は通常融資をしなくなり多くの企業がデフォルトすると考えられます。
この視点を取り入れMertonモデルを改良して作られたのがBlack and Cox(1976)のモデルである(以降、BlackCoxモデルとします)。BlackCoxモデルはエキゾチックオプションであるバリアオプションの理論を応用したモデルであり、企業価値が負債価値に初めて到達した時点でデフォルトと判定するモデルです。
BlackCoxモデルで初めて債務超過した時点でデフォルトすると仮定したことでデフォルトの経路依存性を実現することが出来ました。
しかしBlackCoxモデルでも企業のデフォルトプロセスを十分に表現できてはいません。なぜなら企業は1度債務超過しても企業再建や負債支払い延長などにより延命することがあるからであるからです。実際、鶴田・胥[2005]で分析したデータによると債務超過した企業の平均残存期間は794日であることが述べられています。
つまり理想的には「初めて債務超過した時点である一定数の企業がデフォルトするが、延命する企業もあり、それらの企業群は企業再建に取り組むため、その後の企業価値に依存してデフォルトを判定する」というデフォルト過程を仮定し、定式化する必要があります。
以下にMertonモデル、BlackCoxモデル、そして理想的な構造モデルが想定するデフォルト発生件数分布のイメージを掲載します。

以降では「理想」のデフォルト発生件数分布を近似できるような構造モデルを定式化していきたいと思います。
モデルの定式化
デフォルト発生状況の仮定
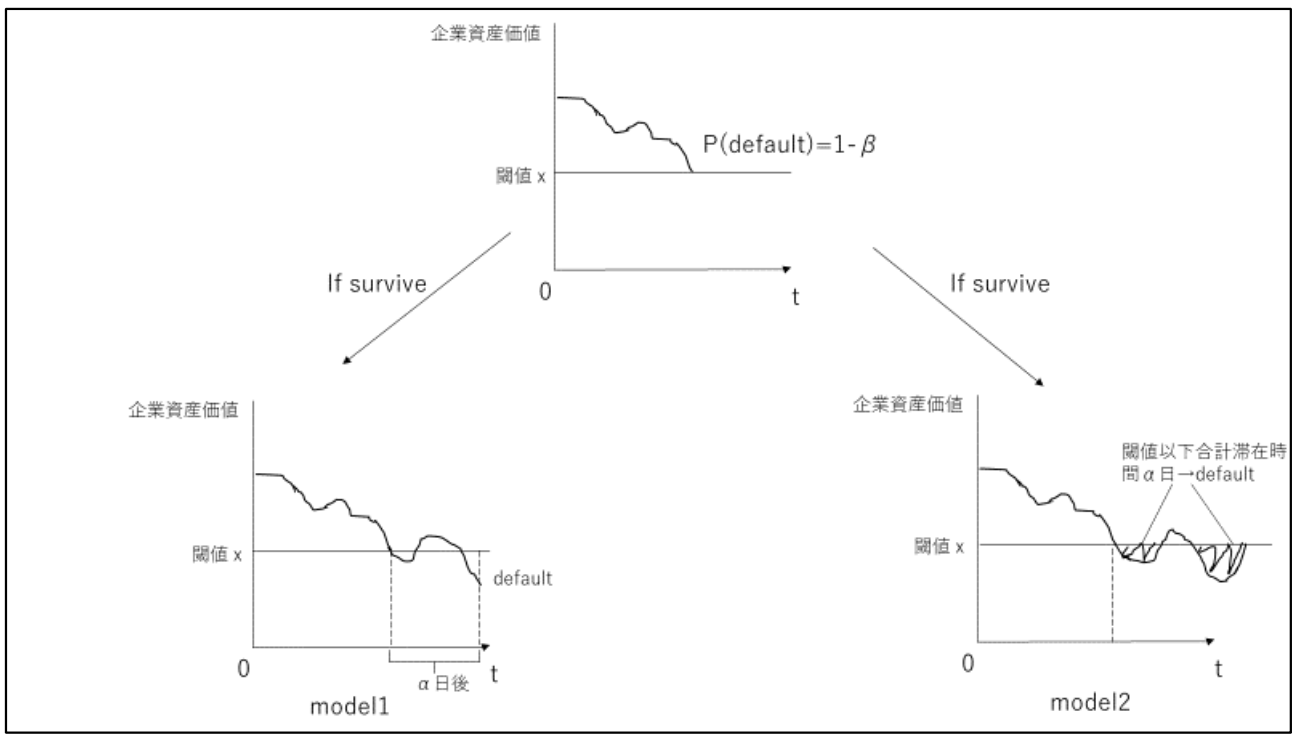
モデルを定式化する上での企業がデフォルトするまでを以下のように仮定します。
- phase1
企業が初めて債務超過した時点でP(default)=1-βのベルヌーイ分布に従ってデフォルト、もしくは延命する。
- phase2
phase1で延命した場合企業再建に努める。企業再建に成功または失敗したかどうかについては以下の判定法1,2で判定する。
- 判定法1:債務超過した日からα日後の企業資産価値が負債価値xを下回っている場合デフォルトとする
- 判定法2:債務超過した日から企業資産価値が合計αT日間デフォルト負債価値xを下回っている場合デフォルトとする
これより判定法1を用いてデフォルト判定を行うモデルをmodel1、判定法2を用いてデフォルト判定を行うモデルをmodel2として定式化していきます。下の図はこの仮定を簡単に図示したものになります。
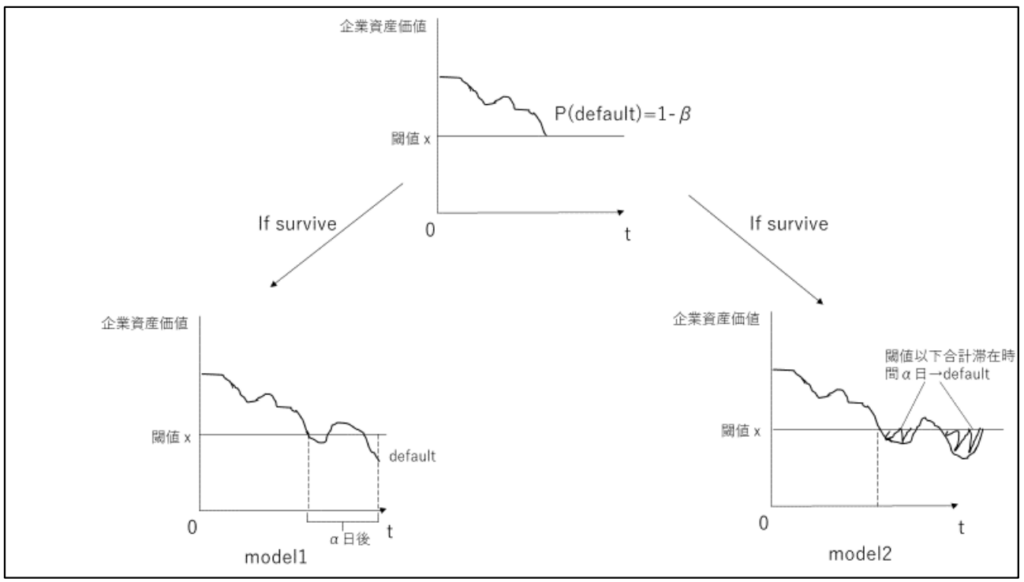
企業価値過程の仮定
森平[2000]において、企業資産市場が完備ではないため従来のリスクフリーレートを用いるのではなく、企業資産の期待収益率をそのまま用いるべきだと指摘されているため、今回は企業価値過程を以下のように設定します。
\(\frac{d A}{A}=\mu_{A} d t+\sigma_{A} d w_{t}\)
ただし、Aを企業価値、\(\mu_{A}\)を企業価値の実期待収益率、\(\sigma_{A}\)を企業価値の標準偏差、w_{t}を実確率の下でのブラウン運動としています。
model1
以下のように定式化することができます。

証明は以下の通りです。

model2
以下のように定式化することができます。

証明は以下の通りです。

パラメータ推定
森平[2000]に倣い、以下のようにパラメータ推定を実施します。
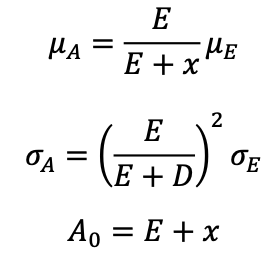
ただし、Eを企業の株価時価総額、𝜇Eを株価収益率、𝜎Eを株価標準偏差としています。
model1、model2のパラメータについては鶴田・胥[2005]で分析したデータを基に次のように設定しました。
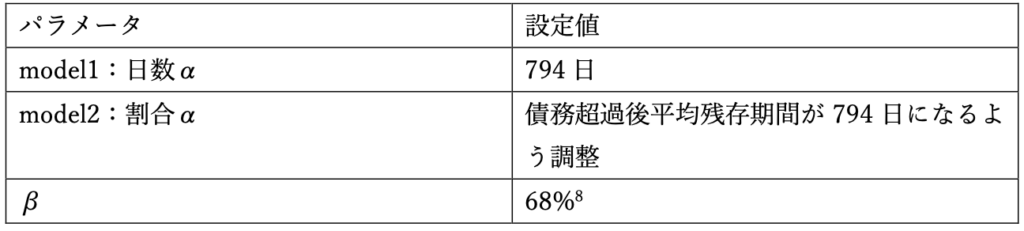
今回は設定を簡単にするために上記のように設定していますが、実際に運用する際は過去データなどから最もフィットする値を設定しても良いと思います。
終わりに
以上、今回は信用リスク評価法における構造モデルを改良し債務超過を許容するように改良しました。
証明部分わかりにくくてスミマセン・・・
次回は今回構築したモデルの精度について従来のMertonモデルやBlackCoxモデルと比較しながら確認していこうと思います。
ご清覧ありがとうございました。