はじめに
以前、当ブログでは強化学習をポートフォリオ最適化に応用する方法について解説しました。
実際に強化学習で資産モデルを構築する際は、
学習方法の決定→モデルの作成→データ収集→モデルのトレーニング→保守・運用
上記のような流れが想定されます。
今回はモデルのトレーニングにおいてどのような方法を用いるのか、トレーニング方法の一つであるDeterministic Policy Gradientについて解説します。
方策関数について
今回も学習方法の決定において前回の記事同様に方策関数ベースの学習方法を採用したと仮定します。
方策関数ベースの場合、運用ウェイトを連続する実数として管理することが可能となりきめ細かい資産運用が可能になります。
方策関数については決定的な方策、つまり確率的ではない方策を考えます。
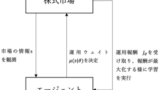
ポートフォリオ管理の場合、株価データなど市場の状態を観測して状態に応じた一意な運用ウェイトを決定するとしても問題ありませんし、むしろ確率的に運用ウェイトを決めてしまうと運用が安定しないなどの副作用も考えられます。
運用ウェイトを決定する以前の情報は、状態として方策関数に入力可能なので、前期の運用ウェイトなどを方策関数に組み込むことをお勧めします。
報酬について
ポートフォリオ最適化に対し強化学習を適用する場合、一般的な深層強化学習に対して大きく異なる点は環境のドメイン知識(環境モデル)が十分に得られており報酬関数が正確に表現できることです。
運用ウェイト×リターン-取引コストで算出することができます。
つまり 方策関数パラメータの更新において報酬関数の勾配を直接算出することが可能であり、更新を容易に実行することができます。
このように報酬関数の勾配を直接計算し、パラメータを更新する方法を Deterministic Policy Gradientと呼びます。
Liang et al.(2018)では、ポートフォリオ最適化において、Deterministic Policy Gradientが様々な学習手法と比較しても最も高いリターンを得ることができることを示しています。
Deterministic Policy Gradient
Deterministic Policy Gradientのアルゴリズムは以下の通りです。

各記号についてはこちらをご覧ください。
- μ:方策関数
- θ:方策関数のパラメータ
- Jθ:報酬(トータルの運用益など)
- st:状態(t期の株価など)
- at:行動(t期の運用ウェイト)
- rt:報酬(t期の運用益)
報酬関数の勾配を直接計算可能であるが故に、項目11番で簡単にパラメータを更新することが可能になります。
終わりに
以上、ポートフォリオ最適化における方策関数学習方法のひとつであるDeterministic Policy Gradientについてご説明しました。
モデルを構築する際など参照いただければ幸いです。
ご清覧ありがとうございました。