LSTMとは
RNNの問題点
以前、当ブログでRNNについて解説しました。
しかし実は、RNNには下記のような問題点があることがわかっています。
- 学習の際、勾配が消失してしまう(勾配消失問題)
- 隠れ層の重みが一定であり、柔軟性がない(入力重み衝突)
勾配消失問題とはRNNのBPTT実行時、過去に遡るにつれて勾配が消失してしまう問題です。
入力重み衝突は時系列データを扱う上での固有の問題として発生します。
通常のニューラルネットワークを学習する場合、関係のある情報が入力された場合、それに応じて重みは大きくし、逆に関係のないデータが入力された場合、それに応じて重みは小さくあるべきです。
しかし、時系列データの場合は現時点の情報は関係ありませんが、将来時点では関係があるというデータが入力された場合、重みは大きくするべきであり、また同時に小さくするべきであるという矛盾を抱えることになってします。
この問題を入力重み衝突といい、RNNの学習がうまくいかない大きな要因となってしまいます。
また同様に出力に関しても出力重み衝突が発生し学習を妨げる原因となることが知られています。
LSTMの設計思想
このような幾つもの課題を解決するためにHochreiter and Schmidhuber(1997)で提案されたのがLSTM(Long Short-Term Memory)です。
LSTMではmemory cellと呼ばれる機構を導入しています。memory cellでは入力ゲート、出力ゲート、忘却ゲートという3つのゲートが作用しており時系列情報をうまくネットワーク内に保持することを可能としています。
LSTM内部構造
まずはmemory cellの構造を以下に示します。
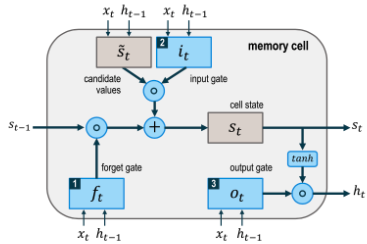
ネットワークの全体像ではなく、あくまでタイムステップtにおけるmemory cellを示したものであることに注意してください。
図よりLSTMは各タイムステップtごとに入力ベクトルxt、内部状態st-1をmemory cellに入力し内部状態であるstを再計算し、次のタイムステップに伝播させるという構造を持っていることがわかります。
また、htはタイムステップtの出力、ft、it、otはそれぞれ忘却ゲート、入力ゲート、出力ゲートを示しています。それぞれのゲートは入力xt、前タイムステップの出力ht-1より計算され、0から1の値をとり、それぞれが以下の様にフィルタとして異なる役割を果たしています。
- 忘却ゲート:前タイムステップから伝播してきた状態st-1の情報をどの程度削除するか指定する
- 入力ゲート:xtの情報をどの程度stに追加するかを指定する
- 出力ゲート:stの情報をどの程度出力するか指定する
言い換えれば、忘却ゲートはリセットの役割、入力ゲートは入力重み衝突を防ぐ役割、出力ゲートは出力重み衝突を防ぐための役割を果たしています。
次にタイムステップtにおけるmemory cellの内部状態st、出力htの算出方法について見ていきます。
まず使用する記号についての説明です。
- xt:タイムステップtにおける入力ベクトル
- Wf,t,Wf,h,Ws,x,Ws,h,Wi,x,Wi,h,Wo,x,Wo,h:重み行列
- bf,bi,bo:バイアスベクトル
- ft:忘却ゲートの値ベクトル
- it:入力ゲートの値ベクトル
- ot:出力ゲートの値ベクトル
- st:タイムステップtにおける内部状態ベクトル
- ht:タイムステップtにおける出力ベクトル
タイムステップtにおいて、まずは前タイムステップからの情報をどの程度削除すべきか決定すべくxt,ht-1bf,Wf,x,Wf,hをもとに以下の様に忘却ゲートの値が計算されます。
ft=sigmoid(Wf,xxt+Wf,hht-1+bf)
ここでsigmoid()はシグモイド関数を表しており、出力を0から1にクリッピングします。
次に内部状態stに対して追加するための情報s’、情報をフィルタリングするための入力ゲートを計算します。
s’t=tanh (Ws’,xxt+Ws’,hht-1+bi )
it=sigmoid(Wi,xxt+Wi,hht-1+bi )
これらをもとにタイムステップtにおける内部状態stを計算します。
st=ft⨀st-1+it⨀s’t
ここで、⨀は行列の要素ごとの掛け合わせるアダマール積を表しています。最後に忘却ゲート、タイムステップtの出力htの計算は以下の様になります。
ot=sigmoid(Wo,xxt+Wo,hht-1+bo)
ht=ot⨀tanh(st)
以上をすべてのタイムステップで繰り返し実行すると、タイムステップの最後の要素の出力がシーケンス全体の最終的な出力として決定されます。
終わりに
以上、今回はRNNの問題点から、LSTMの内部構造まで見てきました。
LSTMの概要は掴んでいただけたかと思うので、より深く学習される方は専門書などの足がかりにしていただけますと幸いです。
ご清覧ありがとうございました。